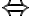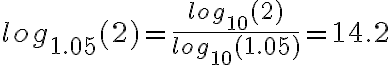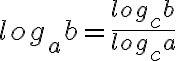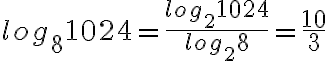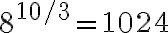Basiswechsel
Basiswechsel
In der Einführung in die Logarithmen haben wir entweder Beispiele verwendet, die man einfach im Kopf lösen kann, oder aber solche mit Basis 10, die mit einem einfachen Taschenrechner berechnet werden können. Das Leben ist aber wie immer nicht ganz so einfach. Oftmals müssen Logarithmen zu beliebigen Basen bestimmt werden.
Stellen Sie sich vor, wir bekommen bei einer sehr grosszügigen Bank 5% Zins. Unser Vermögen multipliziert sich also jedes Jahr mit dem Faktor 1.05. Nach zwei Jahren beträgt der Faktor bereits 1.052, nach drei Jahren 1.053 und so fort. Wir fragen uns, wie lange es geht, bis sich unser Vermögen verdoppelt hat. Diese Fragestellung ist gleichbedeutend mit "Mit welcher Zahl muss man 1.05 potenzieren, um 2 zu erhalten?". Also:
Dies geht weder im Kopf noch direkt mit dem Rechner, denn unsere Taschenrechner können nur für wenige Basen wie 10 oder e direkt Logarithmen berechnen (und 1.05 ist eine sehr unübliche Basis). Es gibt aber einen Trick, den sogenannten Basiswechsel. Nämlich gilt:
(Der letzte Schritt wurde mit dem Taschenrechner ausgeführt.)
Damit wissen wir: In etwas mehr als 14 Jahren wird sich unser Vermögen verdoppeln! Natürlich ist ein Zinssatz von 5% sehr überrissen. Die meisten Banken gewähren 0.25% oder 0.5%. Wie lange müssten Sie dann warten, um das Vermögen zu verdoppeln? (Bei 0.5%: 139 Jahre, bei 0.25%: 277.6 Jahre)
Ganz allgemein gilt:
wobei für c meistens 10 oder e (die Eulersche Zahl) gewählt wird, weil diese beiden Logarithmen standardmässig auf dem Taschenrechner verfügbar sind. Es kann aber irgendeine Basis nach Gutdünken ausgewählt werden - das Resultat verändert sich nicht! Siehe dazu ganz unten das vorgerechnete Beispiel.
Beispiele (zum im Kopf rechnen)
Im folgenden Beispiel wählen wir die Basis 10 für den Basiswechsel:
Also gilt:
Hier wählen wir die Basis 2 für den Basiswechsel:
Also gilt:
Das vorgerechnete Beispiel soll demonstrieren, dass die neue Basis, die für den Basiswechsel gewählt wird, das Resultat nicht beeinflusst. Zuerst wird die Basis 2 und dann die Basis 4 gewählt. Das Beispiel ist so konstruiert, dass die Zahlen aufgehen. Im Prinzip darf aber jede positive, relle Zahl als Basis gewählt werden!