Was ist das, ein Logarithmus?

Logarithmen

Angenommen, Sie bringen einen Franken auf die Bank. Es ist eine sehr (unrealistisch) gute Bank, denn jedes Jahr verzehnfacht sich Ihr Vermögen. Also haben Sie nach einem Jahr 10.-, nach zwei Jahren 100.-, nach drei Jahren 1000.- etc. Nach n Jahren besitzten Sie also

10ⁿ Franken.

Nun möchten Sie wissen, wie viele Jahre n Sie warten müssen, bis Sie eine Million (1'000'000.-) beisammen haben. Die zugehörige Gleichung lautet:

10ⁿ = 1'000'000, n = ?

Wie soll man diese Gleichung nach n auflösen? Die Frage ist:

"Mit welcher Zahl n muss ich 10 potenzieren, um 1'000'000 zu erhalten?" oder "10 hoch wie viel ist 1'000'000?"

Dies ist die Art Frage, auf die Logarithmen die Antwort geben. Als Formel schreibt sich der Logarithmus im vorliegenden Fall so:

n = log₁₀(1'000'000).

Ausgesprochen wird diese Gleichung so: n ist gleich dem Logarithmus von 1'000'000 zur Basis 10.

In diesem Beispiel ist die Lösung n = 6, denn 10⁶ = 1'000'000.

Das war jetzt einfach ein einführendes Zahlenbeispiel, das Ihnen zeigen sollte, wo Logarithmen zum Einsatz kommen. Nun wollen wir das etwas allgemeiner formulieren, denn Sie werden natürlich mit anderen Zahlen konfrontiert werden:

Wenn a hoch x gleich b ist, dann ist x gleich dem Logarithmus von b zur Basis a. Oder als Formel:

x = log_a(b)   $\Leftrightarrow$   a^x = b ,

und die zugehörige Frage lautet: "Mit welcher Zahl muss ich a potenzieren, um b zu erhalten?" oder "a hoch wieviel ist b?". Der Logarithmus ist also immer dann ein heisser Tipp, wenn in einer Aufgabe die Unbekannte irgendwo im Exponenten steht. Die zugehörige Basis muss aber durchaus nicht unbedingt a = 10 sein - es können alle positiven reellen Zahlen eingesetzt werden.

Logarithmen zu speziellen Basen

Der Logarithmus zur Basis 10 ("Zehner-Logarithmus") hat allerdings eine besondere Bedeutung. Das hat mit unserem Zahlensystem zu tun. Das einleitende Beispiel oben hat Ihnen gezeigt, dass der Zehnerlogarithmus von einer Million gerade angibt, wie viele Nullen diese Zahl hat. Der Zehnerlogarithmus wird auch sonst viel gebraucht und hat deshalb eine eigene Schreibweise, nämlich "lg":

log₁₀(x) = lg(x)

Ein weiterer Spezialfall ist der "natürliche Logaritmus" zu Basis e (e = 2.71828... ist eine mathematische Konstante so in der Art wie 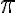$\pi$). Auch dieser Logarithmus ist so wichtig, dass er eine eigene Schreibweise bekommen hat, nämlich "ln":

log_e(x) = ln(x)

Beispiel 1

log₂(32) = x

Gesucht ist also die Zahl x, mit der man 2 potenzieren muss, um 32 zu erhalten: 2^x = 32. In diesem Fall erfüllt x = 5 diese Gleichung: 2⁵ = 32.

Beispiel 2

Gesucht ist die Lösung der Gleichung 5^x = 125. Durch logarithmieren erhält man

x = log₅(125).

Die Lösung ist x = 3 (denn 5³=125).

Beispiel 3

Manchmal sind die Lösungen nicht so augenfällig wie in den obigen Beispielen. Z.B. kann es nötig sein, folgenden Logarithmus zu berechnen:

log₁₀(250) = x

Gesucht ist also die Zahl x, so dass gilt 10^x = 250. Zum Glück haben die gebräuchlichen Taschenrechner eine Taste für den Zehner-Logarithmus. Wenden Sie diese Taste also auf den Wert 250 an. Sie erhalten x = 2.398.

Mehr zum Thema Taschenrechner und Logarithmus hier.

=> Aufgaben zum Thema

=> weiter zu "Basiswechsel"