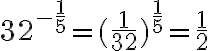Wurzeln
Wurzeln ziehen
Die Quadratwurzel
Wurzelziehen ist quasi die Umkehrung des Potenzierens.Die prominenteste Wurzel ist die Quadratwurzel, d.h. die Umkehrung des Quadrierens. Da beispielsweise 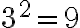 ist, kann man umgekehrt
ist, kann man umgekehrt 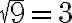 schreiben. Allgemein bedeutet
schreiben. Allgemein bedeutet
das Gleiche wie
Oder zusammengefasst
Die n-te Wurzel
Es gibt allerdings noch andere Wurzeln ausser der Quadratwurzel. Die n-te Wurzel wird dann eingesetzt, wenn das Potenzieren mit n rückgängig gemacht werden soll:
Damit gilt:
So gesehen ist die Quadratwurzel gleich der 2-ten Wurzel, was man aber normalerweise nicht speziell erwähnen muss und darum auch oft nicht schreibt
Potenzschreibweise für Wurzeln
Man kann Wurzeln auch als Potenzen schreiben. Nämlich indem man als Exponenten den entsprechenden Reziprokwert schreibt. Statt ![\sqrt[2]{7} \sqrt[2]{7}](https://moodle.zhaw.ch/filter/tex/pix.php/2b34c530fc7cf41c3ab739cdec6330f3.gif) kann man auch
kann man auch 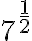 schreiben. Oder allgemeiner:
schreiben. Oder allgemeiner:
Dank der Potenzschreibweise der Wurzel können nun auch "negative Wurzeln" gezogen werden, also z.B. die -n-te Wurzel:
Dies ist nichts anderes als die n-te Wurzel von 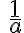 :
:
Zum Mitrechnen:
Nachdem man eine Wurzel in dieser Weise in eine Potenz umgewandelt hat, kann man alle Regeln darauf anwenden, die für Potenzen gelten.
Vorzeichen
Beim Wurzelziehen müssen Sie auf das Vorzeichen aufpassen. Teilweise gibt es zwei Lösungen. 9 hat z.B. zwei Wurzeln, +3 und -3, denn -3 gibt im Quadrat genau so 9 wie 3 im Quadrat! Das vollständige Resultat der Rechnung
ist also: Lösung 1 = +3, Lösung 2 = -3
Keine Lösung hat dagegen die Rechnung
denn es gibt keine Zahl, die beim Quadrieren -9 gibt!
Entsprechendes gilt für alle geradzahligen Wurzeln (also 2.,4.,6. Wurzel etc.).
Bei ungeradzahligen Wurzeln sind die Vorzeichenverhältnisse anders als bei geradzahligen. Z.B. hat
sehr wohl eine Lösung, nämlich -2; denn (-2)3 = -8. Dafür gibt es bei ungeradzahligen Wurzeln immer nur eine Lösung. Das Vorzeichen ist nach dem Wurzelziehen immer das gleiche wie vor dem Wurzelziehen.
Beispiele:

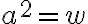
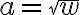
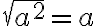
![\sqrt[n]{a^n}=a \sqrt[n]{a^n}=a](https://moodle.zhaw.ch/filter/tex/pix.php/db3f2385441cf655144852d9105708d3.gif)
![x = \sqrt[n]{a} \,\,\Leftrightarrow\,\, x^n = a x = \sqrt[n]{a} \,\,\Leftrightarrow\,\, x^n = a](https://moodle.zhaw.ch/filter/tex/pix.php/7c6d4ef2a2de777706f1b394b4a0e624.gif)
![\sqrt[2]{x}=\sqrt{x} \sqrt[2]{x}=\sqrt{x}](https://moodle.zhaw.ch/filter/tex/pix.php/39a4f78f36d51243541a6a207b8d7bc4.gif)
![\sqrt[n]{a} = a^{\frac{1}{n}} \sqrt[n]{a} = a^{\frac{1}{n}}](https://moodle.zhaw.ch/filter/tex/pix.php/d3c6b07f8140b587861b4eae9597808a.gif)
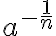
![a^{-\frac{1}{n}} = (a^{-1})^{1/n} = (\frac{1}{a})^{1/n}=\sqrt[n]{\frac{1}{a}} a^{-\frac{1}{n}} = (a^{-1})^{1/n} = (\frac{1}{a})^{1/n}=\sqrt[n]{\frac{1}{a}}](https://moodle.zhaw.ch/filter/tex/pix.php/2db0ea930ccd55684d335f841edbb17f.gif)
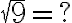
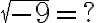
![\sqrt[3]{-8}=? \sqrt[3]{-8}=?](https://moodle.zhaw.ch/filter/tex/pix.php/4d914863320775e164b5c7f3acbe30af.gif)
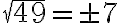
![\sqrt[3]{27} = 3 \sqrt[3]{27} = 3](https://moodle.zhaw.ch/filter/tex/pix.php/66c1f24915ae1cc351a8c411e40ae26a.gif)