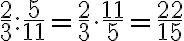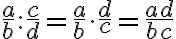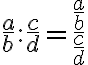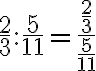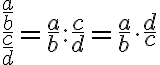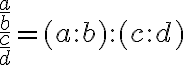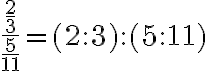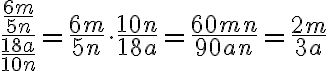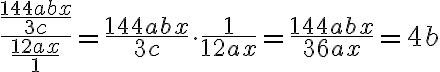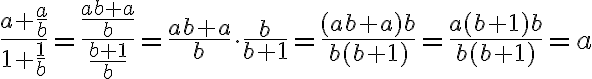Bruch durch Bruch und Doppelbrüche

Bruch durch Bruch

Die Division von Brüchen ist relativ einfach auszuführen, wenn man deren Multiplikation beherrscht: Einfach beim Divisor (demjenigen Bruch, durch den geteilt wird) Zähler und Nenner vertauschen und dann multiplizieren.

Beispiele:

$\frac{2}{3} : \frac{5}{11} = \frac{2}{3} \cdot \frac{11}{5} = \frac{22}{15}$

Mit Variablen:

$\frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{ad}{bc}$

Doppelbrüche

Die Division zweier Brüche kann man selber auch wieder als Bruch schreiben. Das ist dann ein Doppelbruch:

$\frac{a}{b} : \frac{c}{d} = \dfrac{\frac{a}{b}}{\frac{c}{d}}$

$\frac{2}{3} : \frac{5}{11} = \dfrac{\frac{2}{3}}{\frac{5}{11}}$

Man kann das bisherige so zusammenfassen:

$\dfrac{\frac{a}{b}}{\frac{c}{d}} = \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}$

Da ein Bruch selber eine Division darstellt, kann man auch schreiben:

$\dfrac{\frac{a}{b}}{\frac{c}{d}} = (a : b) : (c : d)$

$\frac{\frac{2}{3}}{\frac{5}{11}} = (2 : 3) : (5 : 11)$

Beispiel 1

$\dfrac{\frac{6m}{5n}}{\frac{18a}{10n}} = \frac{6m}{5n} \cdot \frac{10n}{18a} = \frac{60mn}{90an} = \frac{2m}{3a}$

(im letzten Schritt wurde mit 30n gekürzt). Das ganze noch vorgerechnet:

Beispiel 2

$\dfrac{\frac{144abx}{3c}}{\frac{12ax}{1}} = \frac{144abx}{3c} \cdot \frac{1}{12ax} = \frac{144abx}{36 ax} = 4b$

(im letzten Schritt wurde mit 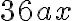$36ax$ gekürzt)

Beispiel 3

Hier werden zuerst Zähler und Nenner separat umgeformt (gleichnamig gemacht) und am Ende wird mit 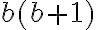$b(b+1)$ gekürzt:

$\dfrac{a+\frac{a}{b}}{1+\frac{1}{b}} = \dfrac{\frac{ab+a}{b}}{\frac{b+1}{b}} = \frac{ab+a}{b} \cdot \frac{b}{b+1} = \frac{(ab+a)b}{b(b+1)} = \frac{a (b+1) b}{b (b+1)} = a$

=> leichte und schwere Aufgaben

=> weiter zu "Umgang mit dem Taschenrechner (Brüche)"

=> gemischte Aufgabenserien (Raum 3)