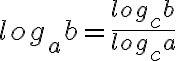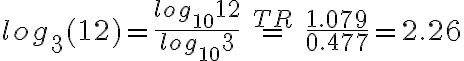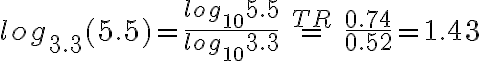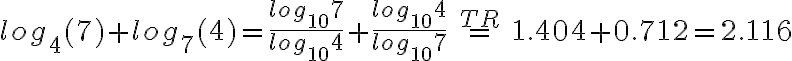Umgang mit dem Taschenrechner
Logarithmen mit dem Taschenrechner
Studientaugliche Rechner sollten mit einer Logarithmusfunktion versehen sein. Üblicherweise können solche Rechner den Logarithmus zur Basis 10 (lg oder log) und zur Basis e (ln) berechnen.
BasiswechselWie im Abschnitt über Logarithmen beschrieben, dürfen Logarithmen zu unüblichen Basen mit dem sogenannten Basiswechsel umgeformt werden:
Dies ist auch im Umgang mit dem Taschenrechner enorm nützlich, wenn die ursprüngliche Basis nicht einer vorprogrammierten Basis entspricht. Man wird daher immer einen Basiswechsel zu 10 oder e vornehmen müssen.
Beispiel 1
TR steht für den Einsatz des Taschenrechners. Diese Lösung kann wiederum so verstanden werden: 3 muss mit 2.26 potenziert werden, um 12 zu erhalten.
32.26 = 12
(Übrigens: Es macht auch intuitiv Sinn, dass diese Zahl zwischen 2 und 3 liegt, denn 32 = 9 und 33 = 27.)
Beispiel 2
Beispiel 3