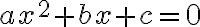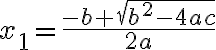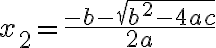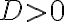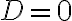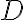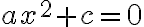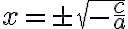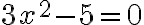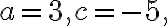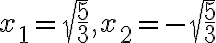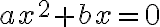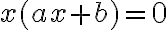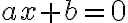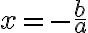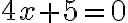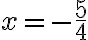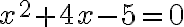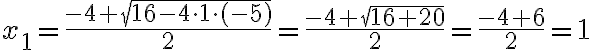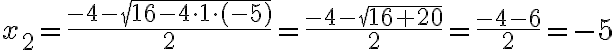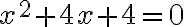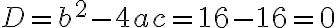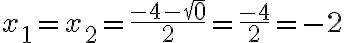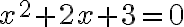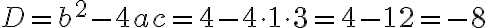Wie löst man quadratische Gleichungen?
Lösen quadratischer Gleichungen
Quadratische Gleichungen sind bereits ein Stück aufwändiger zu lösen als ihre linearen Kollegen. Je nach dem hat eine quadratische Gleichunge keine, eine oder zwei Lösungen. Es kann also durchaus vorkommen, dass die Gleichung keine Lösung hat. Dies bedeutet einfach, dass es dann keine relle Zahl gibt, die man für x einsetzen könnte, damit die Gleichung erfüllt ist.
Schauen wir uns nun die Lösungsformel für quadratische Gleichungen an. Eine solche Gleichung muss immer zuerst in ihre allgemeine Form gebracht werden:
Mit dieser Schreibweise werdenwerden die zwei möglichen Lösungen wie folgt berechnet:
Ob es 2, 1 oder 0 Lösungen gibt, entscheidet sich anhand des Ausdruckes unter der Wurzel, der sogenannten Diskriminante 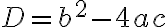 . Nun können drei Fälle eintreten:
. Nun können drei Fälle eintreten:
Es kann auch vorkommen, dass in einer quadratischen Gleichung in der allgemeinen Form einer der Koeffizienten b oder c = 0 ist. Dann kann die Gleichung ohne die Benutzung der komplizierten Lösungsformel aufgelöst werden. Schauen wir uns diese Fälle einmal an:
b=0:
Die Gleichung sieht dann so aus:
Eine kurze Umformung führt zu
Diese Gleichung hat also nur Lösungen, wenn 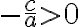 ist, da sonst ein negativer Ausdruck unter der Wurzel steht!
ist, da sonst ein negativer Ausdruck unter der Wurzel steht!
c=0:
Die Gleichung sieht dann so aus:
Hier kann man zunächst 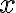 ausklammern:
ausklammern:
und man sieht sofort, dass 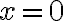 eine Lösung ist (dann wird die Gleichung nämlich zu
eine Lösung ist (dann wird die Gleichung nämlich zu 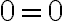 , was sicher eine richtige Aussage ist).
, was sicher eine richtige Aussage ist).
Für die 2. Lösung schaut man was passiert, wenn 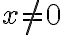 wäre. Dann darf man ja auf beiden Seiten mit
wäre. Dann darf man ja auf beiden Seiten mit 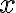 dividieren und es bleibt die lineare Gleichung
dividieren und es bleibt die lineare Gleichung
übrig. Auflösen führt zu
Beispiel: 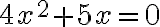
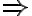
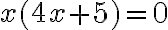 und
und 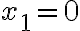 ist eine Lösung. Im anderen Fall
ist eine Lösung. Im anderen Fall 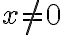 dividieren wir durch
dividieren wir durch 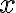 und erhalten
und erhalten
Vorgerechnet:
Beispiel 1 (2 Lösungen):
Hier ist a=1, b=4, c=-5. In die Lösungsformel eingesetzt erhält man die beiden Lösungen
Beispiel 2 (1 Lösung):
Hier ist a=1, b=4, c=4. Berechnen wir zuerst den Wert der Diskriminante:
Da sich die beiden Lösungen x1 und x2 nur in der Diskriminante unterscheiden (einemal wird im Zähler 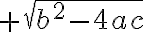 und einmal
und einmal 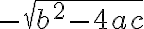 gerechnet), ist x1=x2, d.h. es gibt nur eine Lösung:
gerechnet), ist x1=x2, d.h. es gibt nur eine Lösung:
Beispiel 3 (keine Lösung):
Hier ist a=1, b=2, c=3. Berechnen wir zuerst wieder den Wert der Diskriminante:
Von diesem Ausdruck wird in der Lösungsformel die Wurzel gezogen. Wir wissen aber (siehe Wurzeln), dass die Wurzel einer negativen Zahl keine relle Lösung besitzt. Somit kann keine Lösung berechnet werden und die Gleichung ist unlösbar.
(Bemerkung: die Unlösbarkeit dieser Gleichung gilt im Ihnen bekannten Zahlenraum. Die Mathematiker haben sogenannte "imaginäre Zahlen" erfunden, in denen die Gleichng eine Lösung hätte. Das muss Sie hier aber nicht weiter kümmern - für uns ist die Gleichung unlösbar.)
Beispiel 4
Nachfolgend wird die Gleichung 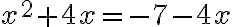 vorgelöst:
vorgelöst: