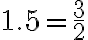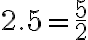Umgang mit dem Taschenrechner

Potenzieren und Wurzelziehen mit dem Taschenrechner

Potenzen

Alle Taschenrechner verfügen über eine Potenzfunktion, wobei wegen seiner Wichtigkeit meistens die Potenz 2 (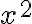$x^2$) eine eigene Taste/Funktion darstellt.

Wurzeln

Wie das Potenzieren gehört auch das Wurzelziehen zur Grundausstattung eines Taschenrechners. Üblicherweise ist eine fixe Funktion oder Taste für die Quadratwurzel vorhanden, sowie eine Funktion für die n-te Wurzel.

Wurzeln aus negativen Zahlen

Probieren Sie, die folgenden Wurzeln der negativen Zahl -15 zu berechnen:

$\,\sqrt[2]{-15}\,$, $\,\sqrt[3]{-15}\,$, $\,\sqrt[4]{-15}\,$, $\,\sqrt[5]{-15}\,$, $\,\sqrt[6]{-15}\,$, $\,\sqrt[7]{-15}\,$

Sie stellen fest: der Rechner weigert sich für gerade n (2, 4, 6) die n-te Wurzel zu ziehen. Dagegen geht dies für ungerade n (3, 5, 7) problemlos (sollte es zumindest). Dieser Tatsache sind wir bereits im Theorieteil über Wurzeln begegnet: aus negativen Zahlen können nur ungerade Wurzeln gezogen werden. Nun haben wir die "Bestätigung" auch vom Rechner erhalten.

Achtung: falls die ungerade Wurzel aus einer negativen Zahl von Ihrem Rechner nicht automatische gezogen wird, müssen Sie künstlich nachhelfen, indem Sie einfach das negative Vorzeichen herausnehmen und den Rechner den Wert aus aus der positiven Zahlen ziehen lassen, also beispielsweise

$\sqrt[3]{-27}=-\underbrace{\sqrt[3]{27}}_{=3} = -3$

Aber Vorsicht: für gerade Wurzeln würde dieses Vorgehen zu einem Fehler führen:

$\sqrt[2]{-16} \neq 4$ !!!

Beispiel 1

Prüfen Sie mit Ihrem Rechner nach:

$\sqrt[5]{97.6} = 2.4997$

$\sqrt[3]{13} \cdot 5^{\frac{1}{5}} = 3.244$

$\sqrt[3]{23^{-2}} = 0.1236$ 

(Tipp: Umschreiben $\sqrt[3]{23^{-2}} = 23^{-\frac{2}{3}}$ und als Potenz berechnen.)

Beispiel 2

Berechnen Sie mit Ihrem Rechner oder im Kopf die vier Werte:  

(-2)¹,  (-2)^1.5, (-2)²,  (-2)^2.5

Hoffentlich weigert sich Ihr Rechner, den 2. und 4. Wert zu berechnen! Wie lässt sich dieses Resultat erklären? Zunächst einmal stellen wir fest, dass die beiden Potenzen 1.5 und 2.5 in Brüche umgeschrieben werden können:

$1.5=\frac{3}{2}$ und $2.5=\frac{5}{2}$

Solchen Bruch-Exponenten sind wir bei den Wurzeln bereits begegnet. Genau genommen versucht man hier wieder, eine gerade Wurzel (wegen dem Nenner=2) aus einer negativen Zahl zu ziehen. Wir haben aber bereits im Beispiel 1 gesehen, dass dies verboten ist!

Wir merken uns: Um Unstimmigkeiten zu vermeiden, sollten keine nicht-ganzzahlige Exponenten für negative Zahlen verwendet werden. Unser Taschenrechner weigert sich zum Glück.

=> Aufgaben zum Thema