Rechnen mit Wurzeln
Rechenregeln für Wurzeln
Für den Umgang mit Wurzeln gibt es wieder Rechenregeln, die man unbedingt beherrschen muss. Es sind eigentlich nur einfach die Rechenregeln für Potenzen in Wurzelschreibweise - Sie haben ja gesehen, dass man Wurzeln auch als Potenzen auffassen kann.
Regel 1: Aus einem Produkt zieht man die (n-te) Wurzel, indem man aus jedem Faktor separat die Wurzel zieht, also z.B.:
Allgemein:
Regel 2: Die (n-te) Wurzel aus einem Bruch zieht man, indem man aus dem Zähler und aus dem Nenner separat die Wurzel zieht, also z.B.:
Allgemein:
Regel 3: Wird eine Wurzel potenziert oder aus einer Potenz die Wurzel gezogen, so kann man die beiden Operationen vertauschen. Z.B.:
Allgemein:
Regel 4: Wird zuerst die m-te Wurzel gezogen und daraus anschliessend noch einmal die (n-te) Wurzel, so kann man dies auch in einem Schritt machen, mit der m·n-ten Wurzel:
Allgemein:
Regel 5: Potenzen, deren Exponent ein Bruch ist, können als Potenz einer Wurzel (oder Wurzel einer Potenz) aufgefasst werden:
Beispielsweise:
Beispiele
Das Letzte noch vorgerechnet:
=> gemischte Aufgaben (Raum 4)
=> weiter zu "Umgang mit dem Taschenrechner (Potenzen und Wurzeln)"

![\sqrt[5]{4\cdot 7}= \sqrt[5]{4}\cdot {\sqrt[5]{7} \sqrt[5]{4\cdot 7}= \sqrt[5]{4}\cdot {\sqrt[5]{7}](https://moodle.zhaw.ch/filter/tex/pix.php/ad752796b170e41f58d36e00761104d4.gif)
![\sqrt[n]{ab} = \sqrt[n]{a}\cdot \sqrt[n]{b} \sqrt[n]{ab} = \sqrt[n]{a}\cdot \sqrt[n]{b}](https://moodle.zhaw.ch/filter/tex/pix.php/908bc48d27f7d11584d369d45ae40d5a.gif)
![\sqrt[5]{\frac{4}{7}} = \frac{\sqrt[5]{4}}{\sqrt[5]{7}} \sqrt[5]{\frac{4}{7}} = \frac{\sqrt[5]{4}}{\sqrt[5]{7}}](https://moodle.zhaw.ch/filter/tex/pix.php/79bb232e0b5a58a95fbcb507f3e5e00f.gif)
![\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}](https://moodle.zhaw.ch/filter/tex/pix.php/7a922c3446debb68c0d058dbbdbc1a74.gif)
![\left(\sqrt[5]{3}\right)^7 = \sqrt[5]{3^7} \left(\sqrt[5]{3}\right)^7 = \sqrt[5]{3^7}](https://moodle.zhaw.ch/filter/tex/pix.php/481ea5208c11b409283e65c01cfc1418.gif)
![\left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m} \left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m}](https://moodle.zhaw.ch/filter/tex/pix.php/c3ce5d0debb201ca8ba3973ceed3d25d.gif)
![\sqrt[4]{\sqrt[5]{3}}=\sqrt[20]{3} \sqrt[4]{\sqrt[5]{3}}=\sqrt[20]{3}](https://moodle.zhaw.ch/filter/tex/pix.php/11352b80c42ecab1f9e2c87a56c1afaf.gif)
![\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a} \sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}](https://moodle.zhaw.ch/filter/tex/pix.php/4eadf8a80885814879b4007bbd7452f0.gif)
![a^{k/l} = \sqrt[l]{a^k} = \left(\sqrt[l]{a}\right)^k a^{k/l} = \sqrt[l]{a^k} = \left(\sqrt[l]{a}\right)^k](https://moodle.zhaw.ch/filter/tex/pix.php/b31011b57fe9df84fdb7cf89a652a773.gif)
![8^{0.6}=8^{3/5} = \sqrt[5]{8^3} 8^{0.6}=8^{3/5} = \sqrt[5]{8^3}](https://moodle.zhaw.ch/filter/tex/pix.php/9ca0ca49c4dccb1d22413c71b1d39022.gif)
![\sqrt[3]{\frac{8}{27}}=\frac{\sqrt[3]{8}}{\sqrt[3]{27}}=\frac{2}{3} \sqrt[3]{\frac{8}{27}}=\frac{\sqrt[3]{8}}{\sqrt[3]{27}}=\frac{2}{3}](https://moodle.zhaw.ch/filter/tex/pix.php/a2979cb68857ebab8dea268100335be3.gif)
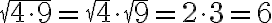
![\underbrace{b}_{\sqrt[3]{b^3}}\cdot \sqrt[3]{\frac{1}{b}} = {\sqrt[3]{b^3} \cdot \sqrt[3]{\frac{1}{b}}= \sqrt[3]{\frac{b^3}{b}} = \sqrt[3]{b^2} = b^{2/3} \underbrace{b}_{\sqrt[3]{b^3}}\cdot \sqrt[3]{\frac{1}{b}} = {\sqrt[3]{b^3} \cdot \sqrt[3]{\frac{1}{b}}= \sqrt[3]{\frac{b^3}{b}} = \sqrt[3]{b^2} = b^{2/3}](https://moodle.zhaw.ch/filter/tex/pix.php/0963479ca94d1bd9df3d812fb9ca18a5.gif)