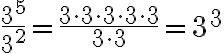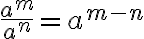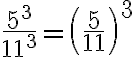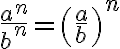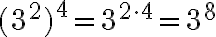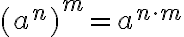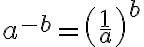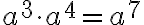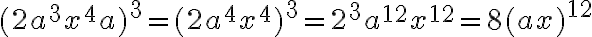Rechnen mit Potenzen

Das Rechnen mit Potenzen

Für den Umgang mit Potenzen gibt es mehrere Rechenregeln, die alles vereinfachen, die man aber auch entsprechend beherrschen muss.

Regel 1: Werden Potenzen mit gleicher Basis miteinander multipliziert, so darf man die Exponenten zusammenzählen. Beispiele:

6^2·6³ = 6⁵

a^2·a⁵ = a⁷

Allgemein:

a^m·aⁿ = a^m+n

Rechnen wir das am obigen Beispiel nochmals nach:

Regel 2:Werden Potenzen mit gleichem Exponenten miteinander multipliziert, so darf man die Basen miteinander multiplizieren. Beispiele:

3²·5² = (3·5)² = (15)²

a⁴·b⁴ = (ab)⁴

Allgemein:

aⁿ·bⁿ = (ab)ⁿ

Rechnen wir das am obigen Beispiel nochmals nach:

Regel 3: Werden Potenzen mit gleicher Basis durcheinander dividiert, so darf man die Exponenten voneinander subtrahieren (Exponenten des Zählers minus Exponent des Nenners). Beispiele:

$\frac{3^5}{3^2} = \frac{3\cdot 3\cdot 3\cdot 3\cdot 3}{3\cdot 3} = 3^3$

Allgemein:

$\frac{a^m}{a^n} = a^{m-n}$

Regel 4: Werden Potenzen mit gleichem Exponenten durcheinander dividiert, so darf man den Exponenten auf den Quotient der Basen anwenden:

$\frac{5^3}{11^3}=\left(\frac{5}{11}\right)^3$

Allgemein:

$\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n$

Regel 5: Wird eine Potenz noch einmal potenziert, so werden die Exponenten miteinander multipliziert:

$(3^2)^4 = 3^{2\cdot 4} = 3^{8}$

Allgemein:

$(a^n)^m = a^{n\cdot m}$

Rechnen wir das nochmals nach:

Der Vollständigkeit halber notieren wir an dieser Stelle noch einmal die Regeln, die Sie schon von der Einführung der Potenzen her kennen:

Regel 6: ein Minuszeichen im Exponenten heisst, dass die Basis durch ihren Kehrwert ersetzt werden soll:

$a^{-b}=\left(\frac{1}{a}\right)^b$

Regel 7: 0 im Exponenten bedeutet, dass die Potenz gleich 1 ist:

a⁰ = 1

Regel 8: 1 im Exponenten bedeutet, dass die Potenz gleich der Basis ist:

a¹ = a

Beispiele

$a^3\cdot a^4 = a^7$

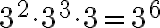$3^2\cdot 3^3 \cdot 3= 3^6$ (Achtung: 3 gilt als 3¹. Dies gilt immer: a=a¹)

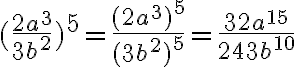$(\frac{2a^3}{3b^2})^5 = \frac{(2a^3)^5}{(3b^2)^5} = \frac{32a^{15}}{243b^{10}}$ (die Potenz 5 gilt auf Zähler und Nenner separat und zudem auf jeden Faktor des Zählers und Nenners.)

$(2a^3x^4a)^3 = (2a^4x^4)^3 = 2^3a^{12}x^{12} = 8 (ax)^{12}$

=> leichte und schwere Aufgaben zum Thema

=> noch mehr Übungen

=> weiter zu "Wurzeln"