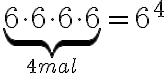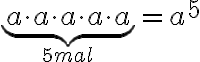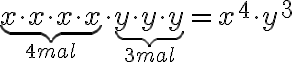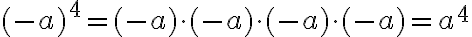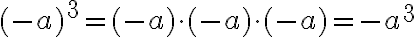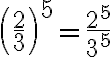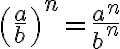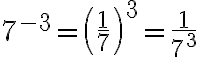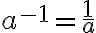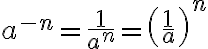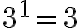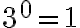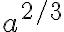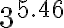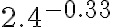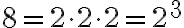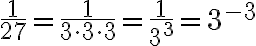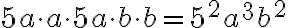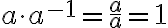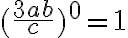Potenzen
Das Potenzieren
Die Potenzschreibweise benutzt man eigentliche einfach aus Bequemlichkeit. Besteht nämlich ein Produkt aus mehreren gleichen Faktoren, so braucht man diese nicht einzeln aufzuschreiben, sondern man kürzt ab mit einer Potenz:
In diesem Beispiel nennt man 6 die Basis, und 4 ist der Exponent. Diese Rechnung gibt beispielsweise an, wie viele verschiedene Zahlenfolgen bei 4 Würfen mit einem Würfel herauskommen können.
Genau gleich rechnet man mit Variablen:
Am häufigsten kommt eine 2 im Exponenten vor, bzw. ein Faktor wird einmal mit sich selber multipliziert. Man spricht in diesem Fall auch von einem Quadrat. b2 spricht man z.B. "b (im) Quadrat" aus.
Es gibt auch Produkte, bei denen verschiedene Basen vorkommen:
Die Basis kann auch negativ sein, wobei die Regel (-)·(-)=+ benutzt werden kann:
Als Regel formuliert:
- Geradzahlige Potenzen (d.h. wenn der Exponent eine gerade Zahl ist) sind immer positiv.
- Ungeradzahlige Potenzen haben das gleiche Vorzeichen wie die Basis.
Potenzen von Brüchen
Die Potenz eines Bruches wird berechnet, indem Zähler und Nenner je zur Potenz erhoben werden:
Negativer Exponent
Der Exponent muss keine positive Zahl sein. Hat eine Potenz einen negativen Exponenten, so ist damit gemeint, dass man die Basis zuerst durch ihren Kehrwert ersetzt und diesen dann potenziert (mit dem Betrag des Exponenten):
Spezielle Exponenten
Speziell zu erwähnen sind auch noch die Exponenten 0 und 1. Es gilt immer:
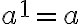 (die erste Potenz ist gleich der Basis)
(die erste Potenz ist gleich der Basis)
und
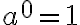 (die nullte Potenz ist gleich 1)
(die nullte Potenz ist gleich 1)
Also beispielsweise
und
Nicht-ganzzahliger Exponent
Der Exponent einer Potenz muss nicht einmal eine ganze Zahl sein. Es ist erlaubt, mit beliebigen Zahlen zu potenzieren, wie z.B.
Manchmal müssen solche Zahlen ausgerechnet werden (jedenfalls dann, wenn keine Variablen vorkommen). Dies geht natürlich nicht im Kopf - wir nehmen den Taschenrechner zu Hilfe.
Beispiele