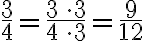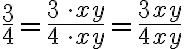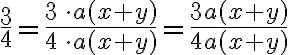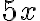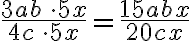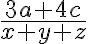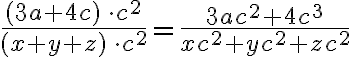Brüche Erweitern
Conditions d’achèvement
Das Erweitern von Brüchen
Die Umkehrung des Kürzens von Brüchen ist das Erweitern. Debei werden Zähler und Nenner eines Bruches mit dem gleichen Term multipliziert, ohne dass sich der Wert des Bruches verändert. Nehmen wir beispielsweise den Bruch 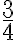 . Der Wert bleibt gleich, wenn man mit 3 erweitert:
. Der Wert bleibt gleich, wenn man mit 3 erweitert:
Analog zum Kürzen dürfen auch beim Erweitern nicht nur Zahlen, sondern auch Variablen benutzt werden:
Beispiel 1
Beispiel 2
Es muss also der ganze Zähler und der ganze Nenner mit 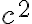 multipliziert werden (jeder Summand der Summe!).
multipliziert werden (jeder Summand der Summe!).
Beispiel 3
Es darf auch mit einem Faktor erweitert werden, der aus einer Summe besteht, z.B. mit 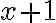 . Dazu wird im folgenden Beispiel
. Dazu wird im folgenden Beispiel 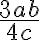 mit
mit 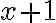 erweitert:
erweitert:
Modifié le: mardi 13 février 2024, 14:37