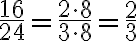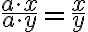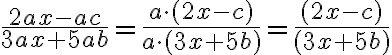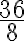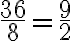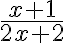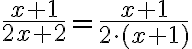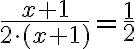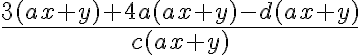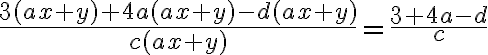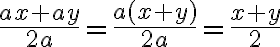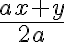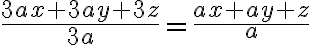Brüche Kürzen
Das Kürzen von Brüchen
Wenn der Zähler und der Nenner eines Bruches gleiche Faktoren enthalten, haben sich diese Faktoren gegenseitig auf. Dann darf der Bruchterm gekürzt werden, ohne dass sich sein Wert verändert:
Einen Bruch zu kürzen, bedeutet nichts anderes, als den Zähler und den Nenner durch die gleiche Zahl zu teilen. Im obigen Fall werden Zähler und Nenner durch 8 geteilt. Dies gilt nicht nur für Zahlen, sondern allgemein für Variabeln. In den folgenden beiden Beispielen wird jeweils mit 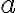 gekürzt:
gekürzt:
Achtung:
-
Es dürfen nur immer Faktoren gekürzt werden, die in gleicher Weise auf den ganzen Zähler und auf den ganzen Nenner wirken.
-
Summanden darf man nicht kürzen!
Demo eines falschen Beispiels an 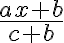 (dieser Ausdruck kann nicht gekürzt werden):
(dieser Ausdruck kann nicht gekürzt werden):
Beispiel 1
Beispiel 2
Hier wird zunächst im Nenner 2 ausgeklammert:
Nun kann man mit (x+1) kürzen:
Fazit: Es darf nicht nur mit einzelnen Zahlen oder Variablen, sondern mit ganzen Faktoren gekürzt werden. In diesem Beispiel ist der Faktor (x+1).
Beachten Sie im diesem Beispiel auch noch, wie der Zähler mit x+1 gekürzt wurde: Es ist dabei nicht etwa 0 übrig geblieben, sondern 1. Auf 0 käme man, wenn man im Zähler (x+1) subtrahierte. Beim Kürzen wird jedoch nicht subtrahiert, sondern dividiert, und (x+1)
Beispiel 3
Hier darf der Faktor 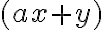 gekürzt werden:
gekürzt werden:
Beispiel 4a
Hier kommt der Faktor 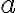 im Zähler und Nenner vor. Er kann zuerst ausgeklammert und dann gekürzt werden:
im Zähler und Nenner vor. Er kann zuerst ausgeklammert und dann gekürzt werden:
Beispiel 4b
Ändert man die Aufgabe leicht ab, so dass der Faktor 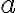 im Zähler nicht mehr in jedem Summanden vorkommt, darf nicht mehr gekürzt werden!
im Zähler nicht mehr in jedem Summanden vorkommt, darf nicht mehr gekürzt werden!
Beispiel 5
Welche Faktoren dürfen hier gekürzt werden?
Hier darf nur mit 3, nicht aber mit a gekürzt werden, weil a im dritten Summanden des Zählers nicht vorkommt. Also:
Beispiel 6
Oftmals wird das Kürzen eines Bruches erst möglich, wenn man im Zähler oder Nenner zuerst etwas ausklammert.
Hier am Beispiel des Bruches 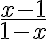 :
: