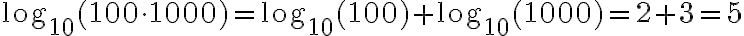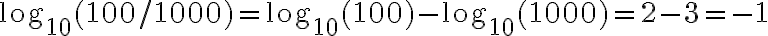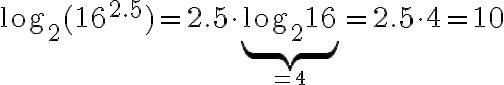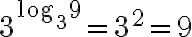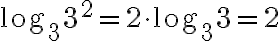Logarithmengesetze (Rechenregeln)

Rechengesetze zum Logarithmus

Im Umgang mit dem Logarithmus müssen drei Rechengesetze beherrscht werden. Wir schreiben im folgenden die Basis jeweils nicht hin, da die Rechenregeln für alle Basen gelten. In der Realität wird dies übrigens oft auch nicht geschrieben da angenommen wird, dass die Basis aus dem Zusammenhang klar ist (Basis 10 oder e=2.71...).

Gesetz 1: Aus dem Produkt wird eine Summe

log(4·5) = log(4) + log(5)

log(a·b) = log(a) + log(b)

Gesetz 2: Aus einer Division wird eine Differenz

log(4/5) = log(4) - log(5)

log(a/b) = log(a) - log(b)

Gesetz 3: Aus einer Potenz wird ein Produkt

log(3⁴) = 4·log(3)

log(a^b) = b·log(a)

Gesetz 4: Der Logarithmus ist die Umkehrung des Potenzierens (logarithmische Identitäten)

(I.)   a^(log_ab) = b

(II.)   log_a(a^b) = b

Beispiele

Gesetz 1:

$\log_{10}(100\cdot 1000)=\log_{10}(100) + \log_{10}(1000) = 2 + 3 = 5$

Gesetz 2:

$\log_{10}(100/1000)=\log_{10}(100)-\log_{10}(1000)=2-3=-1$

Gesetz 3:

$\log_{2}(16^{2.5}) = 2.5\cdot \underbrace{\log_{2}{16}}_{=4} = 2.5\cdot 4 = 10$  

Gesetz 4 (Identitäten):

(I.)  $3^{\log_3 9} = 3^2 =9$

(II.)  $\log_3 3^2 = 2\cdot \log_33 = 2$

Dies noch zum Mitrechnen:

=> Aufgaben zum Thema

=> gemischte Aufgaben (Raum 7)

=> weiter zum Umgang mit dem Taschenrechner (Logarithmen)