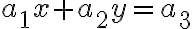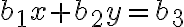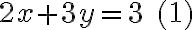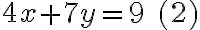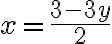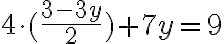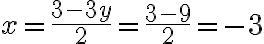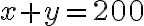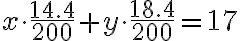Lineare Gleichungs-Systeme
Lineare Gleichungssysteme
Genau so, wie lineare Gleichungen im Zusammenhang mit Proportionalitäten entstehen können, entstehen auch ganze Gleichungssysteme. Ein Gleichungssystem ist einfach eine Sammlung mehrerer Gleichungen, in denen nicht nur eine Unbekannte x vorkommt, sondern mehrere Variablen zu bestimmen sind (die heissen dann vielleicht x, y, z, x1, x2,...).
Hier wird der Fall von 2 Gleichungen mit 2 Unbekannten (x und y) behandelt, aber grundsätzlich können beliebig viele Gleichungen mit der ensprechenden Anzahl Unbekannten aufgelöst werden (also n Gleichungen, n Unbekannte - es ist nämlich ein Gesetz, dass es pro zusätzlicher Unbekannten eine neue Gleichung geben muss, damit es eine eindeutige Lösung geben kann!). In der allgemeinen Form sieht ein System mit n=2 Gleichungen wie folgt aus:
a1, b1, etc. sind dabei Parameter, die in vielen Aufgaben feste Werte annehmen, z.B.:
Ziel ist es, Werte für x und y zu finden, für welche beide Gleichungen gleichzeitig richtig sind. Dazu gibt es verschiedene Methoden. Es ist allerdings etwas Vorsicht geboten, denn es gibt durchaus Fälle, in denen sich die Gleichung nicht oder zumindest nicht eindeutig lösen lässt (aber das ist wiederum eine andere Geschichte...). Hier werden zwei Lösungsmethoden vorgestellt:
a) Substitutionsverfahren
Dies ist die einfacher zu verstehende Methode, allerdings nicht immer die, die am wenigsten zu tun gibt. Das Vorgehen besteht darin, dass zuerst eine der beiden Variabeln bei einer Gleichung freigestellt wird. Beginnen wir mit x aus der obigen Gleichung (1):
Dann wird dieser Ausdruck für x in die Gleichung (2) eingesetzt:
Damit haben wir nur noch eine Gleichung mit einer Unbekannten (siehe vorheriges Kapitel). Der Ausdruck muss nun noch nach y aufgelöst werden und man erhält y = 3. Dieses Ergebnis setzen wir ein in
Die Lösung ist somit:
x = -3, y = 3
b) Eliminationsverfahren
Die zweite Möglicheit, das obige Gleichungssystem zu lösen, ist etwas weniger offensichtlich, aber oftmals recht effizient. Dabei wird eine der Gleichungen so mit geeigneten Wert multipliziert, dass eine der beiden Variablen gerade herausfällt, wenn man die beiden Gleichungen zusammenzählt. Gleichung (1) unseres Beispiels verändert seine Bedeutung ja nicht, wenn man sie beispielsweise mit (-2) multipliziert. Das Gleichungssystem sieht dann so aus:
In der untersten Zeile steht die Summe der beiden Gleichungen. Daraus liest man sofort y = 3 ab. Diese Lösung kann nun in eine der beiden Gleichungen eingesetzt werden, oder man wiederholt das Verfahren für die andere Variable. Möchte man y eliminieren, müssen beide Gleichungen multipliziert werden, nämlich Geichung (1) mit (·7) und Gleichung (2) mit (·3)
Daraus erhält man durch kurzes Umformen x = -3.
Ein Hinweis
Es ist wiederum wichtig zu beachten, dass die Unbekannten x und y in einem linearen Gleichungssystem nicht in einer höheren Potenz vorkommen dürfen - sonst würde es sich um ein nichlineares Gleichungssystem handeln und so etwas behandeln wir hier nicht.
Vorkommen
Lineare Gleichungssysteme ergeben sich oftmals aus physikalischen Zusammenhängen (z.B. Mischaufgaben) oder aus der Prozentrechnung. Beispielsweise führt folgende Fragestellung zu einem Gleichungssystem mit 2 Unbekannten:
Zwei Pralinésorten kosten 14.40Fr. und 18.40Fr. pro 200g. Wie viele Gramm jeder Sorte sollte es in einem 200g Päckli haben, wenn es 17.- kostet?
Setzt man x=Gramm der 1. Sorte und y=Gramm der 2. Sorte, so sieht das Gleichungssystem wie folgt aus:
Man kann nachrechnen, dass x=70g und y=130g die richtige Lösung ist.
Beispiele
Nachfolgend wir das Gleichungssystem
x+y=62x-6=4y-24mit dem Substitutionsverfahren vorgelöst: