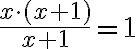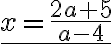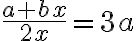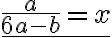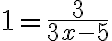Lineare Gleichungen mit einer Unbekannten

Wenn Sie eine Angabe wie z.B. "3 Äpfel kosten 2.-" wörtlich auf Mathematisch übersetzen, landen Sie bei

3·x = 2

(x ist der Preis eines einzelnen Apfels). Sie haben also eine Gleichung vor sich. Und diese Gleichung enthält ein vorerst noch unbekanntes Element (die Unbekannte), nämlich x. Wenn Sie wissen wollen, was der einzelne Apfel kostet, müssen Sie die Gleichung auflösen, d.h. so bearbeiten, dass zuletzt etwas von der Form

x = ...

dasteht, so dass Sie den Apfelpreis ablesen oder direkt ausrechnen können.

Gewiss könnten Sie weniger umständlich herausfinden, was ein Apfel kostet, aber andere Situationen sind weniger übersichtlich, und dann ist der Weg über die Gleichung empfehlenswert oder unumgänglich. Überhaupt landet man in der Mathematik immer und immer wieder bei Gleichungen, die man auflösen soll.

Es gibt verschiedene Kategorien von Gleichungen. In diesem Mathi-Fitness-Studio geht es nur um die beiden wichtigsten und einfachsten Kategorien. Hier können Sie das Auflösen "linearer" Gleichungen trainieren, im nächsten Raum finden Sie dann die quadratischen Gleichungen .


Die Unbekannte wird sehr oft mit x bezeichnet. Sie sollten aber in Erinnerung behalten, dass dies kein Gesetz ist. Vielleicht möchten Sie im Beispiel oben den Apfelpreis mit A abkürzen? Das ist absolut erlaubt, die Wahl der Buchstaben ist frei.

Dass eine Gleichung linear ist, bedeutet folgendes:

die Unbekannte darf mit einer Zahl oder einer Variabeln multipliziert (oder dadurch dividiert) werden; zu diesem Produkt darf noch eine Zahl oder eine Variable addiert (oder subtrahiert) werden; damit haben wir einmal einen linearen Term, d.h. etwas in der Art wie

3x+7

Eine lineare Gleichung ist eine, bei der rechts wie links je ein linearer Term steht, z.B.

3x+7 = 15

(Auch der Term auf der rechten Seite ist linear, denn statt 15 könnten Sie ja auch 0·x+15 schreiben.) Auch eine Gleichung, die man mit einfachem Umstellen in diese Form bringen kann, heisst linear. Damit ist z.B. so etwas gemeint:

\frac{x\cdot (x+1)}{x+1}=1
Wenn man den Bruch links mit (x+1) kürzt, kommt x = 1 heraus, und das entspricht dem Muster linearer Gleichungen.
\quad
Eine lineare Gleichung entsteht immer dann, wenn eine lineare Proportionalität involviert ist. Das Eingangsbeispiel mit dem Apfel illustriert dies: für jeden Apfel muss ich gleich viel bezahlen, für zwei Äpfel also doppelt soviel, für drei das dreifache, etc. Damit können also proportionale Verhältnisse beschrieben werden, denen wir im Alltag oft begegnen und die der Regel folgen "je mehr, desto mehr" oder "je mehr desto weniger", und zwar gleichmässig. Beispielsweise gilt: Je mehr ich arbeite, desto mehr verdiene ich, und zwar gleichmässig mehr. Der Lohn nimmt ja nicht plötzlich schneller oder langsamer zu, wenn ich mehr arbeite, sondern es gilt: doppelte Arbeit, doppelter Lohn! Solche Tatsachen sind oft in linearen Gleichungen versteckt.
 
Beispiele
 
3x - 4 = 2 + 3x - 3 ist eine lineare Gleichung, weil x nur in der 1. Potenz erscheint (also nie als x2, x3 etc.)
3x2 -4x = 3x2 +5 -x ist ebenfalls eine lineare Gleichung, weil sich nämlich der Term 3x2 wegkürzt und damit eine lineare Gleichung übrig bleibt: -4x=5-x
3x2 -4x = 5 -x ist dagegen keine lineare Gleichung, weil der Term 3x2 stehen bleibt. In diesem Fall müssten wir den Lösungsansatz für quadratische Gleichungen benutzen.
 

Wie löst man eine Gleichung auf? Bei jeder Gleichung (auch bei solchen, die nicht linear sind) gilt ein grundlegendes Gesetz:
Sie dürfen mit der rechten Seite einer Gleichung alles machen, was Ihnen einfällt und mathematisch erlaubt ist, und Sie erhalten wieder eine gültige Gleichung - unter einer Bedingung: Sie müssen mit der linken Seite dasselbe tun wie mit der rechten.

Sie können z.B. die obige Gleichung 3x+7 = 15 beidseits mit 3 multiplizieren

3·(3x+7) = 45

oder beidseits mit 5 potenzieren, was immer Sie wollen, nur einfach immer beidseits.
Die Kunst, Gleichungen auflzulösen, besteht meist einfach darin, die Rechenschritte so zu wählen (und auf beiden Seiten korrekt auszuführen), dass die Unbekannte auf einer Seite der Gleichung isoliert wird. Als Beispiel wird dies hier an der Gleichung

5x - 4 = 3x + 2

vorgeführt. Im folgenden wird immer auf beiden Seiten der Gleichung die Operation durchgeführt, die hinter dem Symbol "|" steht:

5x - 4 = 3x + 2 | -3x

=> 2x - 4 = 2 | +4

=> 2x = 6 | : 2

x = 3

In den folgenden Beispielen wird immer nach x aufgelöst.

Beispiel 1

ax - 5 = 4x + 2a | -4x + 5

=> ax - 4x = 2a + 5

x ausklammern:

=> x (a-4) = 2a +5 | : (a-4)

=> \underline{x = \frac{2a+5}{a-4}}

Beachten Sie, dass in dieser Gleichung wie vereinbart x die gesuchte Unbekannte ist, wohingegen a irgendeine Variable ist, die man mit beliebigen Werten belegen kann. Dieses Vorgehen ist oft nützlich, wenn eine allgemeine Lösung einer Gleichung gesucht ist, die dann für alle Werte von a gilt.

Beispiel 2

\frac{a + bx}{2x} = 3a | ·2x

=> a + bx = 6ax | -bx

=> a = 6ax - bx

x ausklammern:

=> a = x (6a - b) | : (6a-b)

\underline{\frac{a}{6a-b} = x}

Beispiel 3

Die Unbekannte kann auch im Nenner eines Bruches stehen:

1=\frac{3}{3x-5}

x wird in diesem Fall aus dem Nenner dieses Bruches zum Verschwinden gebracht, indem die Gleichung geschickt multipliziert wird. Die Lösung sehen Sie hier:

=> Aufgaben zum Thema

=> weiter zu "Textaufgaben"
Modifié le: mardi 13 février 2024, 13:35