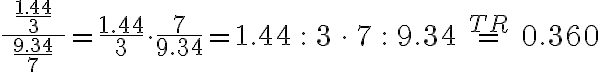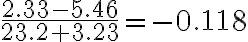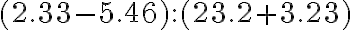Umgang mit dem Taschenrechner

Brüche im Taschenrechner

In vielen Anwendungen möchte man als Resultat eine Kommazahl und nicht einen Bruch stehen lassen (z.B. 1.25 anstatt 5/4). In anderen Situationen stehen im Zähler oder Nenner bereits Kommazahlen, z.B. die Kreiszahl 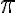$\pi$ oder ein experimentelles Ergebnis. In diesem Zusammenhang wird natürlich nicht mehr im Kopf gerechnet und das Kürzen mit Teilern von ganzen Zahlen kommt so nicht mehr vor. Allerdings gilt für Variablen nach wie vor, dass sie gegeneinander gekürzt werden dürfen (bzw. sollen).

In den nachfolgenden Beispielen bedeutet "TR" jeweils, dass in diesem Schritt der Taschenrechner eingesetzt wird.

Beispiel 1

Im folgenden Beispiel treffen wir eine Mischung zwischen Variablen und Kommazahlen an. Variablen sollten wenn möglich gekürzt werden. Die restlichen Werte können in den Taschenrechner eingegeben werden:

a) 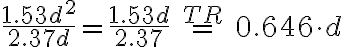$\frac{1.53d^2}{2.37d} =\frac{1.53d}{2.37} \,\stackrel{TR}{=}\, 0.646\cdot d$   (hier wurde mit d gekürzt, d bleibt in Zähler stehen)

b) 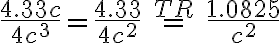$\frac{4.33c}{4c^3} =\frac{4.33}{4c^2} \,\stackrel{TR}{=}\,\frac{1.0825}{c^2}$    (hier wurde mit c gekürzt, c² bleibt in Nenner stehen)

Beispiel 2 (Doppelbrüche)

Doppelbrüche, die Kommazahlen enthalten, werden wie alle anderen Doppelbrüche am besten zuerst in eine Multiplikation verwandelt und danach mit dem Taschenrechner ausgerechnet:

$\frac{\qquad\frac{1.44}{3}\qquad}{\frac{9.34}{7}} = \frac{1.44}{3}\cdot \frac{7}{9.34}=1.44\,:\,3\,\cdot\,7\,:\,9.34 \,\stackrel{TR}{=}\, 0.360$

Beispiel 3 (Klammern und Brüche)

Oftmals stehen im Zähler und Nenner eines Bruches Summen oder Differenzen. Beim Eintippen solcher Terme ist es wichtig, dass dem Rechner durch richtiges Setzen von Klammern mitgeteilt wird, was zusammengehört. Rechnen Sie beispielsweise folgenden Wert mit dem TR aus:

$\frac{2.33 - 5.46}{23.2 + 3.23} = -0.118$

Erhalten Sie das richtige Resultat? Hier ist es wichtig, dass Sie beim Eintippen Klammern benutzen:

$(2.33-5.46) : (23.2+3.23)$

=> Aufgaben zum Thema