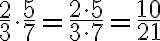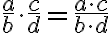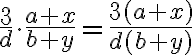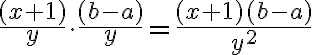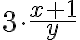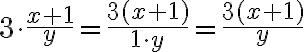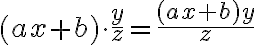Bruch mal Bruch und Bruch mal Zahl
Brüche Multiplizieren
Brüche werden miteinander multipliziert, indem die beiden Zähler und die beiden Nenner je miteinander multipliziert werden. Zum Beispiel:
Und in der Sprache der Variablen:
Vergessen Sie nicht, gegebenenfalls Klammern so zu setzen, dass sich die Multiplikation auf ganze Zähler und ganze Nenner bezieht (so wie in der letzten Gleichung)!
Beispiel 1
Beispiel 2
Hier werden nicht zwei Brüche, sondern eine Zahl mit einem Bruch multipliziert. Eine Zahl darf man auch als Bruch schreiben, nämlich mit Nenner 1. (Division durch 1 ergibt 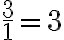 ).
).
Oder anders gesagt: ein Bruch wird mit einer Zahl multipliziert, indem man den Zähler mit der Zahl multipliziert und den Nenner unverändert lässt. Hier noch das Filmli dazu:
Beispiel 3