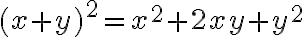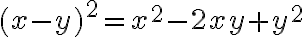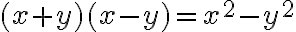Die binomischen Formeln
Die binomischen Formeln
Sonderfälle des Distributivgesetztes treten dann ein, wenn zwei Terme eines Produktes gleich sind:
(x + y)2 = (x + y)·(x + y) = x2 + xy + yx + y2 = x2 + 2xy + y2
Damit haben wir bereits die erste binomische Formel nachgerechnet. Nachfolgend eine Zusammenstellung der drei binomischen Formeln:
Die binomischen Formeln werden so oft gebraucht, dass wir Ihnen empfehlen würden, diese Formeln auswendig zu lernen. Das kostet Sie weniger Zeit, als wenn Sie sie im Laufe der Jahre noch 100 Mal nachschlagen müssen.
Beispiel 1
(3b + 2a)2
Hier entsprechen 3b dem x und 2a dem y aus den binomischen Formeln. Wir berechnen zunächst x2=9b2, 2xy=12ab und y2=4a2. Somit:
(3b + 2a)2 = 9b2 + 12ab + 4a2
Schauen wir uns das noch genauer an:
Beispiel 2
(3x - 4yz)2 = 9x2 - 24xyz + 16y2z2
Beispiel 3
(4ab - 5ac)·(4ab + 5ac) = 16a2b2 - 25a2c2
Beispiel 4
16a4 + 24a2b + 9b2 = (4a2 + 3b)2
=> Aufgaben zum Thema