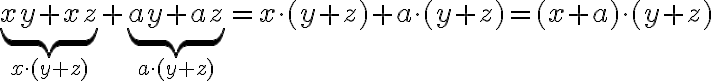Etwas Ausklammern

Ausklammern

Die Schritte des Ausmultiplzierens kann man quasi rückgängig machen. Liest man das Distributivgesetz von rechts nach links, so wird wiederum ausgeklammert. Ausklammern ist immer dann möglich, wenn alle Summanden einen gemeinsamen Faktor besitzen:

15 + 10 = 5(3 + 2) (gemeinsamer Faktor 5)

xy + xz = x(y + z) (gemeinsamer Faktor x)

3am² + 3bm² + 3cm² = 3m²(a + b + c) (gemeinsamer Faktor 3m²)

Es kann auch vorkommen, dass ausgeklammert werden kann, wenn die Summanden keinen gemeinsamen Faktor enthalten. Im folgenden Beispiel werden zunächst x und a ausgeklammert und danach der Summand (y + z):

$\underbrace{xy + xz}_{x\cdot (y + z)} + \underbrace{ay + az}_{a\cdot (y + z)} = x\cdot (y + z) + a\cdot (y + z) = (x + a)\cdot (y + z)$

Liest man diese Rechnung rückwärts, erkennt man gerade wieder das Distributivgesetz!

Beispiele

8xy - 4xz = 4x·(2y - z)   (gemeinsamer Faktor 4x)

12a - 10b + 4 = 2·(6a - 5b +2)   (gemeinsamer Faktor 2)

a(x-y) + b(x-y) = (a+b)·(x-y)   (gemeinsamer Faktor (x-y))

Bemerkung: Der ausgeklammerte Faktor kann vor oder hinter der Klammer der restlichen Ausdrück geschrieben werden. Wegen dem Kommutativgesetz der Multiplikation gilt ja beispielsweise im letzten Beispiel:

(a+b)(x-y) = (x-y)(a+b)

Zwischen den Klammern steht ein ungeschriebenes Malzeichen!

=> Aufgaben zum Thema

=> weiter zu den binomischen Formeln