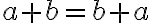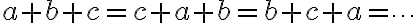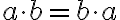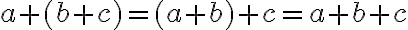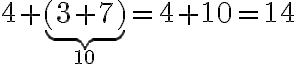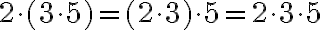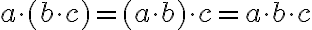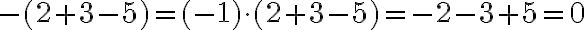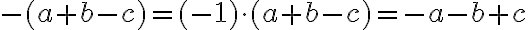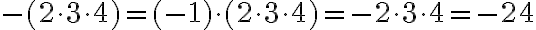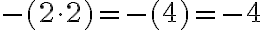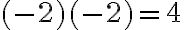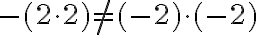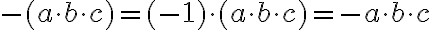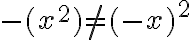Die Grundoperationen
Das Kommutativgesetz
Beim Addieren ("plus rechnen") kommt es nicht auf die Reihenfolge der Summanden an. 2+4 gibt bekanntlich das gleiche wie 4+2. Mit Variablen statt Zahlen ist das nicht anders:
Das Kommutativgesetz gilt auch für die Multiplikation:
2·3 = 3·2
Das Assoziativgesetz
In Summen mit mindestens drei Summanden können Klammern beliebig gesetzt werden. Diese Eigenschaft der Addition nennt man assoziativ. Klammern weisen darauf hin, dass der eingeschlossene Term zuerst ausgerechnet werden soll, bevor mit der Berechnung weitergefahren wird. Beispiele:
Das Assoziativgesetz gilt auch für die Multiplikation:
Auflösen von Klammern
Ein negatives Vorzeichen vor einer Klammer, die einen Summenterm enthält, bedeutet eine Multiplikation jedes Summanden mit -1 (Distributivgesetz, siehe auch hier):
Ein negatives Vorzeichen vor Klammern vor einer Klammer, die einen Produktterm enthält, stellt einen zusätzlichen Faktor -1 dar:
Achtung: Im obigen Beispiel wirkt das - nicht auf einzelne Faktoren, sondern auf den ganzen Ausdruck in der Klammer! Darum wird das Resultat negativ. Etwas anderes wäre es, wenn (-2) mit sich selber multipliziert würde:
Also:
Und mit Buchstaben:
Prüfen wir die letzte Ungleichheit nochmals nach: