Vorkurs Physik
Abschnittsübersicht
-
In diesem Abschnitt lernen Sie, ein Ort-Zeit-Diagramm zu zeichnen. Ausserdem lernen Sie, wie man gleichförmige (mit konstanter Geschwindigkeit) und gleichmässig beschleunigte Bewegung auf einer geraden Linie mathematisch beschreibt. Dann lernen Sie, wie man von der Position zur Geschwindigkeit zur Beschleunigung und umgekehrt gelangt.
-
Das Ort-Zeit-Diagramm Theorie
Schauen Sie das Video zu Ort-Zeit-Diagram an (2 Minuten) und machen Sie dann die Aufgaben.
-
Das Ort-Zeit-Diagramm Aufgabe
Nehmen Sie Ihre Bewegungsdiagramm hervor, die Sie in dem vorangegangenen Abschnitt konstruiert haben und zeichnen Sie dann für jede der unten genannten Aufgaben ein Ort-Zeit-Diagramm. Benutzen Sie dazu je nach Aufgabenstellung Ihre Bewegungsdiagramme. Um Ihre Lösung zu kontrollieren, klicken Sie einfach auf die Aufgabe.
Bewegt sich ein Objekt über eine bestimmte Strecke mit konstanter Geschwindigkeit nach rechts, so ist seine Geschwindigkeit positiv. Sein Ort-Zeit-Diagramm ist dann eine Gerade die nach rechts oben zeigt (positive Steigung). Bewegt es sich schneller, so wird die Gerade steiler (Steigung grösser).
Bewegt sich ein Objekt nach links, so ist seine Geschwindigkeit negativ (entgegen der x-Achse gerichtet). Sein Ort-Zeit-Diagramm ist eine Gerade die nach unten rechts zeigt (negative Steigung). Umso schneller es sich bewegt, umso steiler ist die Gerade (Steigung negativer).
Das Objekt bewegt sich nach rechts, also auf der positiven Richtung der x-Achse. Es wird dabei immer langsamer, also wird auch die Steigung des Ort-Zeit-Diagramms immer kleiner. Die Kurve zeigt nach rechts oben und flacht ab.
Das Objekt bewegt sich nach links, deshalb liegen alle Punkte auf der negativen Seite der Achse. Es wird immer schneller, das heisst, die Steigung der Kurve wird immer grösser. Die Kurve wird immer steiler.
Bei der Aufwärtsbewegung wird das Objekt abgebremst: Die Geschwindigkeit zeigt nach oben, ist also positiv. Die Steigung der Kurve ist positiv. Die Geschwindigkeit und damit auch die Steigung nehmen ab. Die Kurve wird immer flacher. Am obersten Punkt ist die Geschwindigkeit null. Die Steigung der Kurve ist auch null, sie ist ganz flach. Dann sinkt das Objekt wieder. Seine Geschwindigkeit und auch die Steigung der Kurve sind negativ. Sie nimmt ab. Das Objekt wird immer schneller. Die Geschwindigkeit und auch die Steigung werden immer negativer, die Kurve wird immer steiler. -
Gleichförmige Bewegung Theorie
Schauen Sie sich das Video zur gleichförmigen Bewegung an (6 min) und machen Sie die Aufgaben im Anschluss.
-
Gleichförmige Bewegung Aufgabe
Testen Sie Ihr Wissen zur gleichförmigen Bewegung. -
Momentangeschwindigkeit und Geschwindigkeit-Zeit-Diagramm Theorie
Schauen Sie sich das Video zur Momentangeschwindigkeit an (5 min) und machen Sie die Aufgaben im Anhang.
-
Momentangeschwindigkeit und Geschwindigkeit-Zeit-Diagramm Aufgabe
Nehmen Sie Ihre Ort-Zeit-Diagramme, die Sie in dem Abschnitt oben konstruiert haben und zeichnen Sie für jedes der Diagramme ein Geschwindigkeits-Zeit-Diagramm. Um Ihre Lösung zu kontrollieren, klicken Sie einfach auf die Aufgabe.
Bewegt sich ein Objekt über eine bestimmte Strecke mit konstanter Geschwindigkeit nach rechts, so ist sein Geschwindigkeits-Zeit-Diagramm eine horizontale Gerade durch einen positiven Wert.
Bewegt sich ein Objekt über eine bestimmte Strecke mit konstanter Geschwindigkeit nach links, so ist sein Geschwindigkeits-Zeit-Diagramm eine horizontale Gerade durch einen negativen Wert.
Das Objekt bewegt sich zuerst mit konstanter Geschwindigkeit nach rechts (positives Geradenstück). Dann nimmt die Geschwindigkeit ab.
Das Objekt bewegt sich nach links, deshalb ist seine Geschwindigkeit negativ. Es wird immer schneller, die Geschwindigkeit nimmt immer negativere Werte an. Ab dem Punkt, wo die Geschwindigkeit konstant ist, ist das Geschwindigkeits-Zeit-Diagramm ein horizontales Geradenstück.
Die Geschwindigkeit zeigt nach oben, ist also positiv. Die Geschwindigkeit nimmt bei der Aufwärtsbewegung ab. Am obersten Punkt ist die Geschwindigkeit null. Dann sinkt das Objekt wieder. Seine Geschwindigkeit ist jetzt negativ. Das Objekt wird immer schneller. Die Geschwindigkeit nimmt immer negativere Werte an. -
Von der Geschwindigkeit zur Position Theorie
Schauen Sie sich das Video (5,5 min) an. Es zeigt Ihnen wie Sie die Position eines Objektes berechnen können, wenn Sie ein Geschwindigkeits-Zeit-Diagramm haben. Anschliessend machen Sie die Aufgaben im Anhang.
-
Von der Geschwindigkeit zur Position Aufgaben
In der Abbildung unten ist das Geschwindigkeit-Zeit-Diagramm eines Objektes gezeigt. Zeichnen Sie das Ort-Zeit-Diagramm, wenn das Objekt sich zum Zeitpunkt t=0 s am Ort x=-8 m befindet.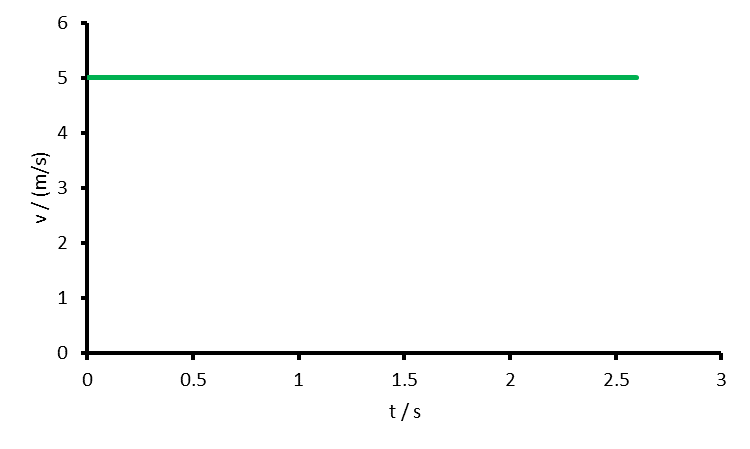
Das Ort-Zeit-Diagramm ist eine Gerade mit Steigung 5 und Achsenabschnitt -8
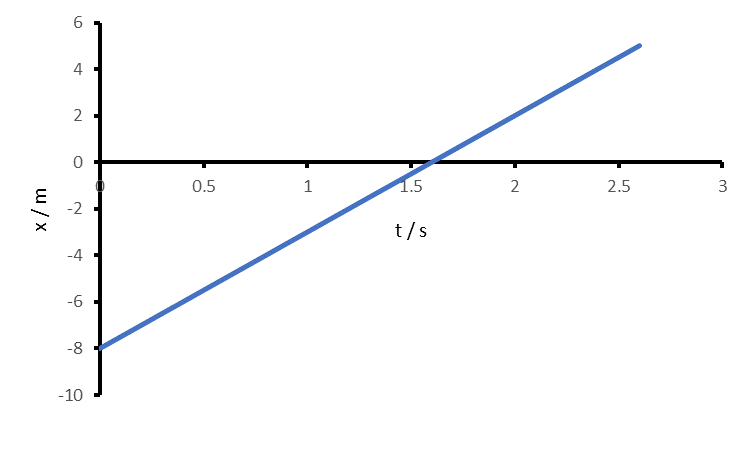
-
-
In der Abbildung unten ist das Geschwindigkeit-Zeit-Diagramm eines Objektes gezeigt. Zeichnen Sie das Ort-Zeit-Diagramm, wenn das Objekt sich zum Zeitpunkt t=0 s am Ort x=8 m befindet.
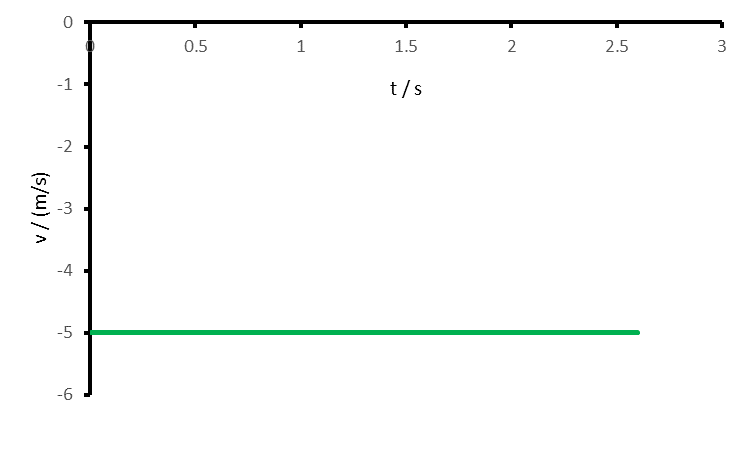
Das Ort-Zeit-Diagramm ist eine Gerade mit Steigung -5 und Achsenabschnitt 8
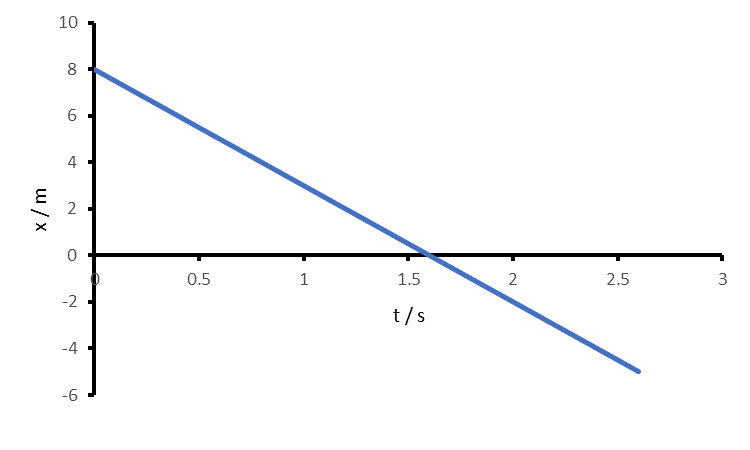
-
-
In der Abbildung unten ist das Geschwindigkeit-Zeit-Diagramm eines Objektes gezeigt. Zeichnen Sie das Ort-Zeit-Diagramm, wenn das Objekt sich zum Zeitpunkt t=0 s am Ort x=2 m befindet.
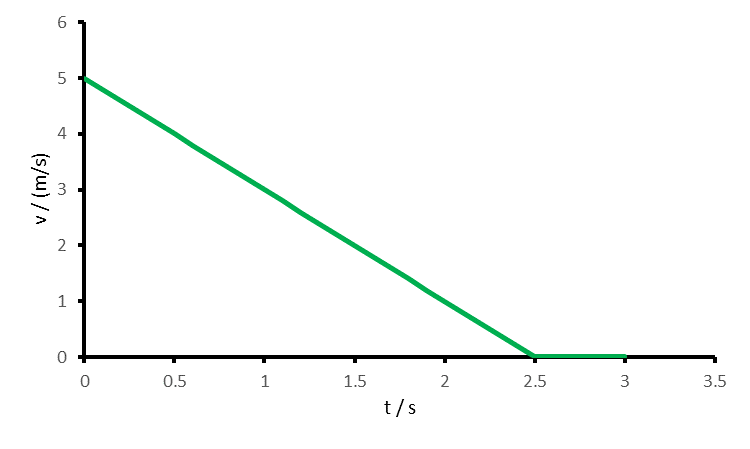
Das Ort-Zeit-Diagramm ist eine Parabel. Das Objekt wird immer langsamer. Bei t=2.5 s ist die Geschwindigkeit null. Das Objekt bewegt sich nicht mehr. Das Ort-Zeit-Diagramm ist ab hier horizontal. Die Verschiebung des Objekts bis zum Zeitpunkt t=2.5 s berechnet sich mit Hilfe der Fläche des Dreiecks: 0.5*(2.5 s)*(5 m/s)=6.25 m
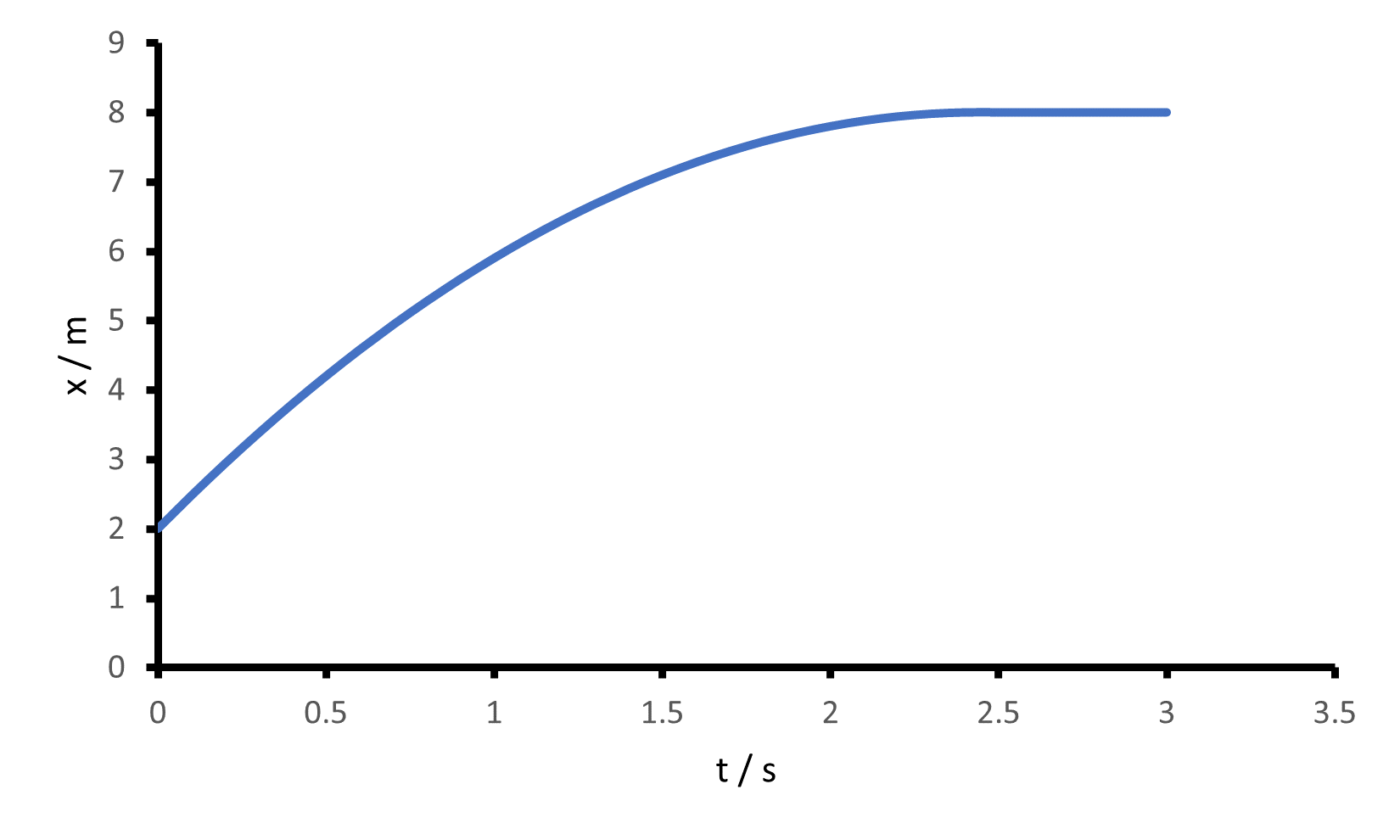
-
-
In der Abbildung unten ist das Geschwindigkeit-Zeit-Diagramm eines Objektes gezeigt. Zeichnen Sie das Ort-Zeit-Diagramm, wenn das Objekt sich zum Zeitpunkt t=0 s am Ort x=-4 m befindet.
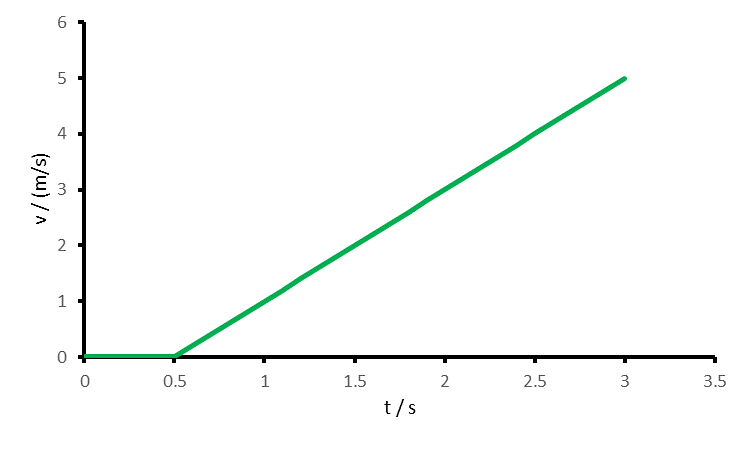
Bis zum Zeitpunkt t=0.5 s ist die Geschwindigkeit des Objekts null. Es bleibt am Ort x=-4 m stehen. Dann beschleunigt das Objekt. Die Steigung des Ort-Zeit-Diagramms nimmt stetig zu. Es handelt sich ab diesem Punkt um eine Parabel. Die Verschiebung des Objekts zwischen t=0.5 s und t=3 s berechnet sich mit der Fläche des Dreiecks zwischen der v-t-Kurve und der t-Achse 0.5*(2.5s)*(5 m/s)=6.25 m.
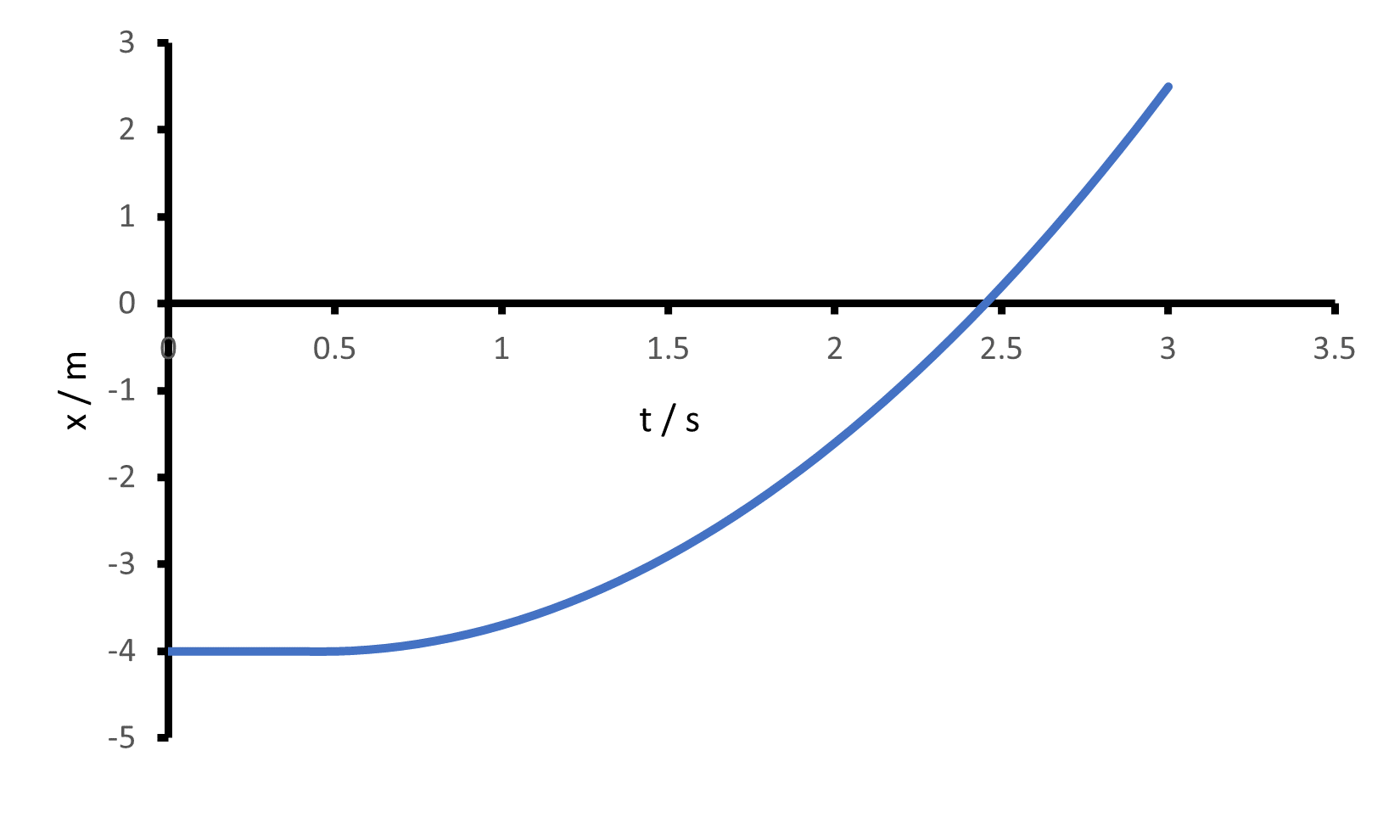
-
Die gleichmässig beschleunigte Bewegung Theorie
Schauen Sie sich das Video zur gleichmässig beschleunigten Bewegung (4 min) an und machen sie die Aufgaben im Anhang.
-
Die gleichmässig beschleunigte Bewegung Aufgabe
Testen Sie Ihr Wissen zur gleichmässig beschleunigten Bewegung -
Momentanbeschleunigung Aufgabe
Ordnen Sie den a-t-Diagrammen die entsprechenden v-t-Diagrammen zu
-