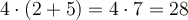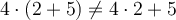Rechnen mit Klammern
Abschlussbedingungen
Rechnen mit Klammern
Regel 1: Der Ausdruck in der Klammer muss zuerst ausgerechnet werden.
Klammern werden üblicherweise dazu verwendet, um die Zusammengehörigkeit der darin vorhandenen Zahlen oder Symbole zu unterstreichen. Wenn etwas zahlenmässig ausgerechnet wird, haben Klammern einen Einfluss auf die Reihenfolge der Rechenschritte: Was in einer Klammer steht, soll zuerst berechnet werden. Beispielsweise bedeutet 4·(2+5), dass 4 mit der ganzen Klammer multipliziert werden soll. Also:
Falsch wäre, 4 nur mit 2 zu multiplizieren: 4·2+5 = 13. Ohne Klammer hätte der Ausdruck also eine andere Bedeutung:
Bei ineinander verschachtelten Klammern fängt man zuinnerst an und arbeitet sich nach aussen:
Zuletzt geändert: Dienstag, 13. Februar 2024, 13:20